You might remember the y-intercept of any graph is just the point at which the curve or line passes through the y-axis. So in the picture below. Point Q is the y-intercept of the parabola.

The y-intercept is a point (?,?), and you need to find both coordinates. But if you thought about it for a second, you already know one of them.....yes, you know the x-coordinate is zero. Why? Because if it wasn't then it wouldn't be on the y-axis. It would be a point somewhere on either side of the y-axis.
So cool, you already have half the answer. You know the y-intercept is (0,?). Now, remember, whenever you have one coordinate of a point, and you know the equation you can always plug the coordinate you know into the equation and find the other. So to find the y-coordinate, just plug zero in for all the x's.
Let's see this in action. Let's take the quadratic function . If we want to find the y-intercept, we remember we already know the y-intercept is (0,?). So we plug in zero for the x's and solve for y.
. If we want to find the y-intercept, we remember we already know the y-intercept is (0,?). So we plug in zero for the x's and solve for y. 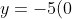^{2}+2(0)-5)
Simplifying the equation,
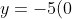+2(0)-5)
Then,
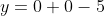
so
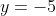
That means the y-intercept is (0,-5)
Also see:
-intro to 11.6
-the direction/orientation of the parabola
-the vertex of the parabola
-the line of symmetry
-the x-intercepts

The y-intercept is a point (?,?), and you need to find both coordinates. But if you thought about it for a second, you already know one of them.....yes, you know the x-coordinate is zero. Why? Because if it wasn't then it wouldn't be on the y-axis. It would be a point somewhere on either side of the y-axis.
So cool, you already have half the answer. You know the y-intercept is (0,?). Now, remember, whenever you have one coordinate of a point, and you know the equation you can always plug the coordinate you know into the equation and find the other. So to find the y-coordinate, just plug zero in for all the x's.
Let's see this in action. Let's take the quadratic function
Simplifying the equation,
Then,
so
That means the y-intercept is (0,-5)
Also see:
-intro to 11.6
-the direction/orientation of the parabola
-the vertex of the parabola
-the line of symmetry
-the x-intercepts
No comments:
Post a Comment