Every parabola has a vertex. Depending on the orientation of the parabola, it will always be the highest or lowest point on the parabola. Here is a picture of two parabolas graphed on the same coordinate plane with the vertices labeled.

The first thing you should remember is that the vertex is a point. And points look like this (3,5) Therefore you have to find two coordinates, the x-coordinate and the y-coordinate.
Step 1: Finding the x-coordinate of the vertex
If you are given a quadratic equation, say . All you have to do is note a,b, and c.
. All you have to do is note a,b, and c.
a = -5
b = 2
c = -5
And then use a little formula. to calculate the x-coordinate of the vertex.
to calculate the x-coordinate of the vertex.
In our example, is
is  . Simplifying,
. Simplifying,  which is 1/5. So we know this much about our vertex now, it is a point (1/5, ?)
which is 1/5. So we know this much about our vertex now, it is a point (1/5, ?)
Step 2: Finding the y-coordinate of the vertex
One tends to forget this, but whenever you have one coordinate of a point, and you know the equation you can always plug the coordinate you know into the equation and find the other. So in our case, we know the x-coordinate, we are going to plug it into our quadratic function, and find out our y-coordinate. In step 1 we figured out that the x-coordinate is 1/5 and we also have our function . So, watch the magic, we just plug in 1/5 for every "x" in our function:
. So, watch the magic, we just plug in 1/5 for every "x" in our function: 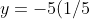^{2}+2(1/5)-5) . Now we simplify the right side,
. Now we simplify the right side,
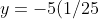+2/5-5)
some more
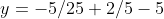
and some more
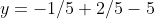
and...
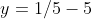
finally!
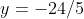
There's our y-coordinate!
So our vertex is (1/5, -24/5)
Here is a little demo I did from a question in the homework. (Watch out there is an embarrassing bit of subtraction in there. The y-coordinate should be -10, not -18.)
Also see:
-intro to 11.6
-the direction/orientation of the parabola
-the line of symmetry
-the y-intercept
-the x-intercepts

The first thing you should remember is that the vertex is a point. And points look like this (3,5) Therefore you have to find two coordinates, the x-coordinate and the y-coordinate.
Step 1: Finding the x-coordinate of the vertex
If you are given a quadratic equation, say
a = -5
b = 2
c = -5
And then use a little formula.
In our example,
Step 2: Finding the y-coordinate of the vertex
One tends to forget this, but whenever you have one coordinate of a point, and you know the equation you can always plug the coordinate you know into the equation and find the other. So in our case, we know the x-coordinate, we are going to plug it into our quadratic function, and find out our y-coordinate. In step 1 we figured out that the x-coordinate is 1/5 and we also have our function
some more
and some more
and...
finally!
There's our y-coordinate!
So our vertex is (1/5, -24/5)
Here is a little demo I did from a question in the homework. (Watch out there is an embarrassing bit of subtraction in there. The y-coordinate should be -10, not -18.)
Also see:
-intro to 11.6
-the direction/orientation of the parabola
-the line of symmetry
-the y-intercept
-the x-intercepts
No comments:
Post a Comment