Finding the x-intercept/s of a quadratic function

You might remember an x-intercept of any graph is just a point at which the curve or line passes through the x-axis. So in the picture below. Point P and R are the x-intercepts of the parabola.

An x-intercept is a point (?,?), and you need to find both coordinates. But if you thought about it for a second, you already know one of them.....yes, you know the y-coordinate is zero. Why? Because if it wasn't then it wouldn't be on the x-axis. It would be a point somewhere above or below the x-axis.

So cool, you already have half the answer. You know the x-intercept is (?,0). Now, remember, whenever you have one coordinate of a point, and you know the equation you can always plug the coordinate you know into the equation and find the other. So to find the x-coordinate, just plug zero in for y.

Let's see this in action. Let's take the quadratic function . If we want to find the x-intercept, we remember we already know the x-intercept is (?,0). So we plug in zero for y and solve for x.

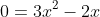
Now, how do we solve this for x? You guessed it, it's time for the quadratic formula. I got x = 2/3 and 0. What this means is this parabola has two x-intercepts (2/3,0) and (0,0).

Also see:
-intro to 11.6
-the direction/orientation of the parabola
-the vertex of the parabola
-the line of symmetry
-the y-intercept