Finding the line of symmetry

You might have noticed every parabola has a line of symmetry running down it's middle.

The line of symmetry is always a vertical line no matter whether the parabola is an "uppie" or "downie". Vertical lines have a funny form, they are always written x = n, where n is just some number. Here's an example,

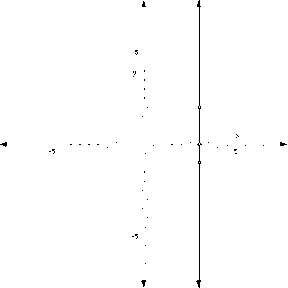
This line's equation is x=3.

How do we find the vertical line that is a parabola's line of symmetry? We observe that the line of symmetery always runs through the vertex of the parabola, so whatever the x-coordinate of a parabola's vertex is, that will give you the equation of the parabola's line of symmetry.

Let's see an example. Take the quadratic function . We note
a= 3
b= -2
c= 0
Then we find the x-coordinate of our vertex using the formula -b/(2a). {Note: this is detailed in a previous post}. -b/(2a) = 2/(2*3) = 2/6 = 1/3. So we know this much about our vertex (1/3, ?). We could go on and find the y-coordinate of the vertex, but we have all we need to know to write the line of symmetry.
It's x = 1/3.


Also see:
-intro to 11.6
-the direction/orientation of the parabola
-the vertex of the parabola
-the y-intercept
-the x-intercepts