Finding the orientation of a quadratic function

Are you an "uppy" or a "downy"? All quadratic functions are either oriented up, like this

or down, like this
.
Ever seen the "downies" on the side of the road?

Now if you are given a particular quadratic function like . All you need do is make sure it is the standard quadratic function form 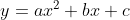and note what a, b, and c are. For our example,
a=-5
b=2
c=-5
To tell if it is an "uppy" or "downy", just look at "a". If "a" is positive, the parabola is an "uppy". If it's negative, the parabola is a "downy". So in our example, a = -5, so our parabola is a "downy".

Another example, has
a= 3
b= -2
c = 0
Since "a" is positive, this parabola is an "uppy".


Also see:
-intro to 11.6
-the vertex of the parabola
-the line of symmetry
-the y-intercept
-the x-intercepts